数学,这门看似抽象却与人类文明息息相关的学科,即便严格来说不属于科学范畴,却是科学大厦得以稳固搭建和不断攀升的坚实基石。从人类懵懂的牙牙学语时期开始,便已在潜移默化中接触到最基本的数学概念。当孩子长到两三岁,不少人就能熟练地从 1 数到 100,甚至能进行简单的加减运算,这足以见得数学与人类的紧密联系是与生俱来的。
然而,追溯人类数学思想的源头,一个关键问题始终萦绕在学者心头:人类究竟从何时开始拥有数的概念?这个问题至今没有确切答案。

更令人困惑的是,我们甚至无法确定数学是随着人类文明的崛起而逐步形成的产物,还是深藏于人类意识之中,通过日常经验不断总结提炼出的逻辑基础。这一谜题,为数学的历史增添了几分神秘色彩。
从现存的人类古代文献来看,最早的计数工具其实极为简单,“结绳计数” 便是其中典型的代表。在那个生产力水平低下、文字尚未普及的时代,人们通过在绳子上打结的方式来记录数量,比如用不同数量的绳结代表不同数量的猎物、粮食等。这种看似原始的计数方式,实则是一种相当简洁且实用的数学表达方式,它体现了古人对数量关系的初步认知,也是人类数学思想萌芽的重要见证。
从结绳计数这种计数方式中,我们不难发现古人对大自然的认知秉持着一种古朴而纯粹的态度。

他们倾向于用简洁的整数去理解和描述世间万物,坚信整数能够完美地代表自然界中的各种数量关系。在相当长的一段时间里,这种 “简洁自然美” 的认知在人们的思想中占据着主导地位,成为当时数学发展的潜在思想指引。
但当人们对直角三角形的三条边展开深入研究时,这种看似完美的认知被彻底打破,一个不协调的现象出现在人们眼前,而这一发现也成为了人类数学认知史上第一次变革的导火索。那么,这个不协调的现象究竟是什么呢?
我们不妨做一个假设:假设有一个两条直角边长度都为 1 的等腰直角三角形,按照我们现在所学的数学知识,运用勾股定理(直角三角形的两条直角边的平方和等于斜边的平方)可以轻松算出,它的斜边长应该是根号 2。

根号 2 是一个无理数,这在如今是众所周知的常识,但在古代,人们对无理数毫无概念。当古人尝试计算根号 2 的具体数值时,他们陷入了前所未有的困惑与抓狂之中。在计算过程中,他们发现这个数的小数部分无穷无尽,无论花费多少时间去计算,都看不到尽头,这与他们之前所认知的简洁整数截然不同。
根号 2,作为人类发现的第一个无理数,它的出现犹如一颗重磅炸弹,彻底颠覆了古人对数学的认知,也酿成了人类历史上的第一次数学危机。

无理数的存在,击碎了古人心中 “简洁自然美” 的完美幻想,让他们难以接受这个事实。在当时的人们看来,根号 2 这种无限不循环的小数是如此 “怪异”,甚至被视为 “邪恶” 的象征。
但无论人们多么抵触,根号 2 这个数的客观存在是无法被忽视的,古人不可能像掩耳盗铃般对其视而不见。为了弄清楚无理数背后的奥秘,人们开始将目光投向物理学领域,希望通过对物理现象的深入研究来找到答案。正是在这个过程中,人类第一次接触到了 “无穷” 的概念,并且由此诞生了著名的四大悖论之一 —— 芝诺悖论。
相信很多人都听说过芝诺悖论,它以一种看似合理却与现实相悖的逻辑,引发了人们对运动和无穷的深刻思考。芝诺悖论中有一个经典的关于赛跑的例子:假设你和一只乌龟进行赛跑,由于乌龟的速度远远慢于你,所以设定的出发点并不相同,乌龟在你前方 100 米的位置。已知你的速度是乌龟速度的 10 倍。

那么,按照现实情况来看,你显然能够追上并超越乌龟,毕竟你的速度具有明显优势,用不了多久就能追上乌龟。但根据芝诺悖论的逻辑推理,你却永远不可能追上乌龟,这究竟是为什么呢?
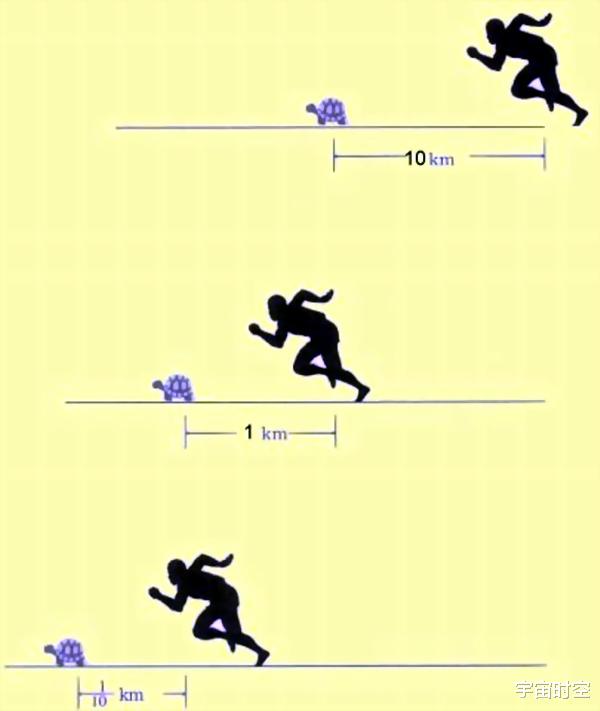
芝诺悖论是这样分析的:乌龟一开始就领先你 100 米,当你奋力跑完这 100 米,终于到达乌龟最初的出发点时,在这段时间里,乌龟并没有静止不动,它又向前跑了 10 米;接着,当你继续跑完这 10 米,朝着乌龟新的位置追赶时,乌龟又向前移动了 1 米;之后,当你跑完这 1 米,乌龟再次向前跑了 0.1 米…… 就这样循环往复,按照这种逻辑推演下去,乌龟似乎永远都在你前面,你跑过的路程始终只是乌龟之前跑过的路程,这就意味着你永远也追不上乌龟。
可现实情况我们都非常清楚,你很快就能追上并超越乌龟,为什么理论推演和现实之间会出现如此明显的 “矛盾” 呢?问题到底出在哪里?
古人对芝诺悖论展开了深入的思考和探讨,在这个过程中,“无穷” 的概念得到了进一步的延伸和发展,同时人们也逐渐发现了芝诺悖论所存在的漏洞。实际上,芝诺悖论更像是一种巧妙的 “诡辩”,它刻意设定了一个看似合理的 “陷阱” 让人们陷入其中。

其关键问题在于,芝诺悖论忽略了时间的有限性。在现实生活中,我们的时间是有限的,根本不可能在有限的时间里完成无穷多的事情,而芝诺悖论却假设人们可以在有限时间内无限次地追赶,这显然与现实情况不符。正是认识到了这一点,人们才成功避免了跳进芝诺悖论设定的 “陷阱”。
随着人们对无理数以及无穷概念的不断探索和深入研究,人类历史上的第一次数学危机终于得以成功化解。这次危机的化解,不仅让人们对数学的认知迈上了一个新台阶,也为数学的后续发展奠定了坚实的基础,使得人类数学在之后的近 2000 年时间里,都处于一个相对稳定、平静的发展状态,直到牛顿和莱布尼茨的出现,打破了这种平静。
牛顿和莱布尼茨的重大贡献,便是共同创立了微积分。

微积分的诞生,犹如一场数学革命,彻底改变了数学的发展轨迹,同时也引发了人类历史上的第二次数学危机。
微积分在数学乃至整个科学领域的作用都极为重大,它的出现为解决许多之前被认为无法解决的难题提供了全新的思路和方法。例如,在微积分出现之前,人们很难精确测量那些形状曲折、不规则图形的面积,也无法准确计算弯曲曲线的长度。而有了微积分之后,这些难题都迎刃而解,人们可以轻松地通过微积分的方法来实现精确测量,这极大地推动了数学、物理学、天文学等众多学科的发展。
在很多人眼中,微积分听起来高深莫测,理解起来也十分困难,充满了 “高大上” 的气息。但实际上,微积分的思想基础并非那么复杂,其核心思想就是 “无限细分然后再整合”。简单来说,就是将一个复杂的问题分解成无数个微小的部分,对这些微小部分进行研究和计算,然后再将这些结果整合起来,从而得到整个问题的答案。而微积分的基础,便是无限逼近零的概念。
在微积分的应用过程中,人们常常会在很多情况下直接将无限小当做零来使用,却并没有真正搞清楚无限小和零之间的本质区别以及它们所蕴含的数学含义。在牛顿和莱布尼茨所处的时代,无论是微分、积分,还是导数,人们对这些概念的真正含义都没有形成清晰、准确的认识,相关的理论基础也不够完善,这就为第二次数学危机的爆发埋下了隐患。
虽然第二次数学危机在很早之前就已经得到了解决,但直到今天,仍然有很多人对微积分相关概念存在不理解,甚至存在误解。要理解第二次数学危机,我们可以从一个最简单的例子入手,那就是:0.999…… 和 1 哪个更大?

可能很多人会下意识地认为 0.999…… 小于 1,但实际上,正确的答案是 0.999…… 和 1 一样大,因为从数学的严格定义和逻辑推理来看,0.999…… 和 1 完全就是同一个数,只是表达方式不同而已。然而,即便如此,直到今天,仍旧有不少人坚持认为 0.999…… 小于 1。对于这种常见的误解,我们可以简单粗暴地总结:认为 0.999…… 小于 1 的人,基本上是完全没有理解 “无穷” 概念的内在含义。

当然,这并不是要怪罪或者嘲笑那些不理解的人,毕竟在我们的日常生活中,所接触到的都是有限的事物,我们的认知和经验大多建立在有限的范畴之内。而 “无穷” 的概念本身就超越了日常经验的范畴,很多时候都与我们的日常生活认知相悖,我们的潜意识往往会不自觉地让我们接受那些符合日常生活经验的认知,这就导致理解 “无穷” 概念变得十分困难。
说到底,第二次数学危机的根源,就在于人们对微积分的理论基础以及 “无穷” 概念的理解存在偏差。随着数学学科的不断发展,数学家们通过建立更加严谨的数学理论体系,比如实数理论、极限理论等,才最终彻底解决了第二次数学危机,让微积分有了坚实、可靠的理论支撑。
在人们成功诠释第二次数学危机两百多年后,数学领域又迎来了一次巨大的挑战,第三次数学危机悄然爆发。而引发这次危机的,是一个著名的悖论 ——“罗素悖论”,通过这个悖论,我们可以清晰地了解第三次数学危机的核心内容。

在罗素悖论中,有一个广为人知的例子:有一位技术精湛的理发师,他在宣传自己的理发服务时这样打广告:“我会给所有不能给自己理发的人理发!”
这个广告语看似简单,却蕴含着一个令人困惑的逻辑问题:这位理发师会给自己理发吗?如果我们假设理发师会给自己理发,那么根据他的广告语 “给所有不能给自己理发的人理发”,他就不应该给自己理发,这就产生了矛盾;如果我们假设理发师不会给自己理发,那么按照他的承诺,他就应该给自己理发,同样陷入了矛盾之中。无论我们给出 “会” 还是 “不会” 的答案,都会与理发师的广告语相互矛盾。
其实,罗素悖论所体现的逻辑矛盾,与 “上帝悖论” 有着异曲同工之妙。

“上帝悖论” 是这样表述的:人们认为上帝是无所不能的,那么上帝能创造出一块他自己搬不动的石头吗?如果答案是能,那么上帝无法搬动自己创造的石头,这就说明上帝并非无所不能;如果答案是不能,那么上帝无法创造出这样一块石头,同样证明上帝不是无所不能的。无论回答 “能” 还是 “不能”,都会与 “上帝无所不能” 的前提产生矛盾。
从本质上讲,罗素悖论更偏向于一种哲学思想的体现,它与哲学中的本体论有着密切的联系,甚至可以从罗素悖论延伸出唯心主义和唯物主义的相关思考。那么,从哲学角度来看,罗素悖论究竟想表达什么呢?
通俗地说,罗素悖论的特点在于,它总是在一开始将某个对象(比如理发师)置身于某个事件或范畴之外,然后紧接着又换一种角度,将这个对象重新纳入到该事件或范畴之中。

这种看似矛盾的设定,实际上是自己制造了逻辑冲突:这个对象到底处于什么位置?是在事件或范畴之内,还是之外呢?
如果用主观唯心主义的观点来解读罗素悖论,我们可以做这样的假设:假设整个世界都是由你的意识幻想出来的表象,也就是说,宇宙中的万事万物,包括你身边的人、周围的环境等,都是你的意识所构建出来的虚幻景象。那么,一个关键的问题就出现了:“你” 本身这个概念,也是你的意识幻想出来的假象吗?
如果答案是肯定的,即 “你” 的概念是意识幻想的产物,那么进一步思考就会发现,“你对‘你’的概念产生质疑的这种思想”,是不是也同样是由你的意识幻想出来的呢?
看到这里,相信大家已经察觉到其中的问题了,这样的推理结果就像俄罗斯套娃一样,一层套一层,永远没有尽头。最终,这个问题会演变成一个终极哲学难题:你的意识本体到底是什么?它存在于哪里?
如果承认你的意识是存在的,那么就会陷入上述无限循环的矛盾之中;而如果认为你的意识不存在,那么按照之前的假设,由你的意识幻想出来的整个世界也就不复存在了,这又与我们所感知到的现实世界相矛盾。
严格来说,罗素悖论并非真正意义上的数学问题,它更多的是对数学中集合定义的一种 “诡辩”。所谓的诡辩,说白了就是一种看似有理有据,实则违背逻辑规律的 “抬杠” 行为。令人遗憾的是,直到今天,人们也没有找到一个完美的方法来彻底解决这类诡辩问题。
第三次数学危机的爆发,让数学家们意识到数学的基础理论体系还存在着漏洞和不完善之处。

为了解决这次危机,数学家们纷纷投入到对数学基础的研究之中,试图建立更加严谨、无矛盾的数学体系。在这个过程中,集合论得到了进一步的发展和完善,公理化集合论的出现,在一定程度上缓解了罗素悖论带来的冲击,为数学基础的稳固做出了重要贡献。但即便如此,关于数学基础的讨论和研究从未停止,数学家们依然在不断探索,希望能够找到一个更加完美的解决方案,推动数学学科朝着更加成熟、完善的方向发展。
从第一次数学危机中无理数的出现,到第二次数学危机围绕微积分展开的争论,再到第三次数学危机中罗素悖论引发的对数学基础的思考,每一次危机的爆发都给数学领域带来了巨大的冲击,但同时也成为了数学发展的重要契机。每一次危机的化解,都促使数学的理论体系更加严谨、完善,推动着数学学科不断向前迈进。在未来,数学或许还会面临新的挑战和危机,但正是这些挑战和危机,将不断激发数学家们的探索热情,推动数学这门古老而又充满活力的学科持续发展,为人类文明的进步做出更大的贡献。