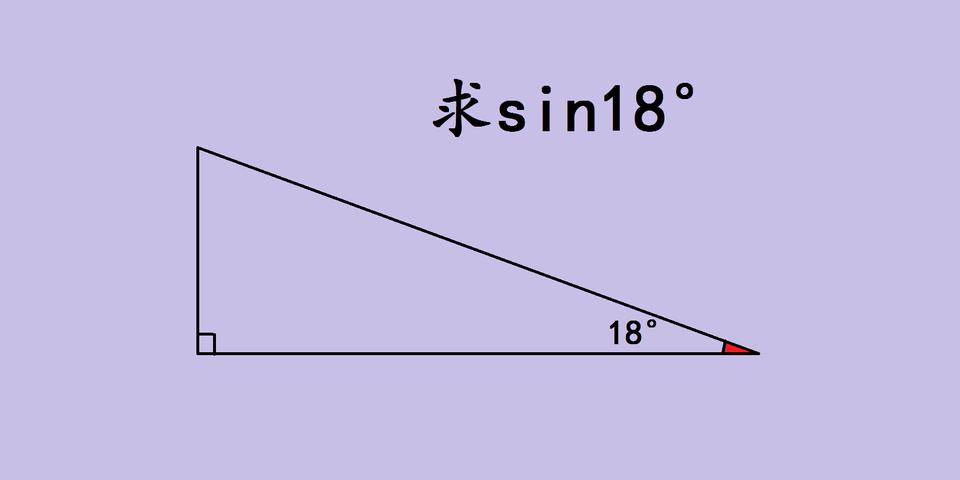
初中竞赛｜求sin18°的核心思维：用黄金三角形搭起几何与代数的桥 求sin18°是初中竞赛里的经典难题，它的突破点不在于硬算，而在于“构造黄金三角形”的巧思。 18°的两倍是36°，而黄金三角形（顶角36°、底角72°的等腰三角形）刚好能完美容纳这个角度。我们可以先构造一个黄金三角形，再通过作角平分线或高线，把18°角自然嵌入图形中。 此时，相似三角形会成为关键工具：黄金三角形被分割后，会出现多个相似的小等腰三角形。通过对应边成比例的关系，我们能把线段长度的比例转化为代数方程，从而推导出18°角对边与斜边的比值——也就是sin18°的表达式。 这道题的核心思维，是“几何构造+代数转化”的跨界联动：从三角函数的需求出发，用黄金三角形搭建几何模型，再借相似三角形完成线段到方程的过渡。这种思路不只是解这一道题，更能帮孩子建立“用几何直观解决代数问题”的思维习惯，为高中三角函数的学习埋下伏笔。 要不要我帮你整理一份黄金三角形构造步骤清单，让你更清晰地理解这个思维过程？