精心构造的输入样本能让机器学习模型产生错误判断，这些样本与正常数据的差异微小到人眼无法察觉，却能让模型以极高置信度输出错误预测。这类特殊构造的输入在学术界被称为对抗样本(adversarial examples)。

模型将右侧图像判定为长臂猿，置信度高达99.3%。

人眼看不出这两张熊猫图像有任何区别，而模型对左图的预测是熊猫，置信度57.7%显得不太确定。中间那张看起来像噪声的图案其实是经过精心设计的扰动掩码，将其乘以一个很小的系数0.007后叠加到原图上。肉眼完全察觉不到变化，但却可以让模型以99.3%的置信度认定右图是长臂猫的图像。

这个现象说明模型并未真正理解图像的本质结构。模型构建的是一种内部表征来描述自然图像，但分布外的数据点就能轻易突破这种表征的局限。

2014年Christian Szegedy做过一个有趣的实验：他从CIFAR-10数据集选了几张图片，试图用反向传播把它们逐步转换成飞机，想观察图像是如何一步步接近飞机的样子。

结果的图像几乎没什么变化，但右下角这张在视觉上依然是辆车的图片，模型却近乎百分百确信它是架飞机。

视觉模型的输入维度通常很高，每个像素的微小改变累积起来会在表征向量中产生显著变化，用L₂范数可以直观看出这种累积效应。

几乎所有机器学习模型都存在对抗攻击的脆弱性：逻辑回归、softmax回归、支持向量机这类线性模型特别容易被精心设计的样本误导；相比之下径向基函数(RBF)这种高度非线性的模型抵抗力要强一些。

多数机器学习模型的线性特性恰恰为生成对抗样本做了最好的理论铺垫，RNN和LSTM用加法操作来捕捉时序数据的流动，加法本质上是线性的；而ReLU、maxout这些激活函数让深度神经网络的输入输出关系呈现分段线性特征。

进一步看这个过程：

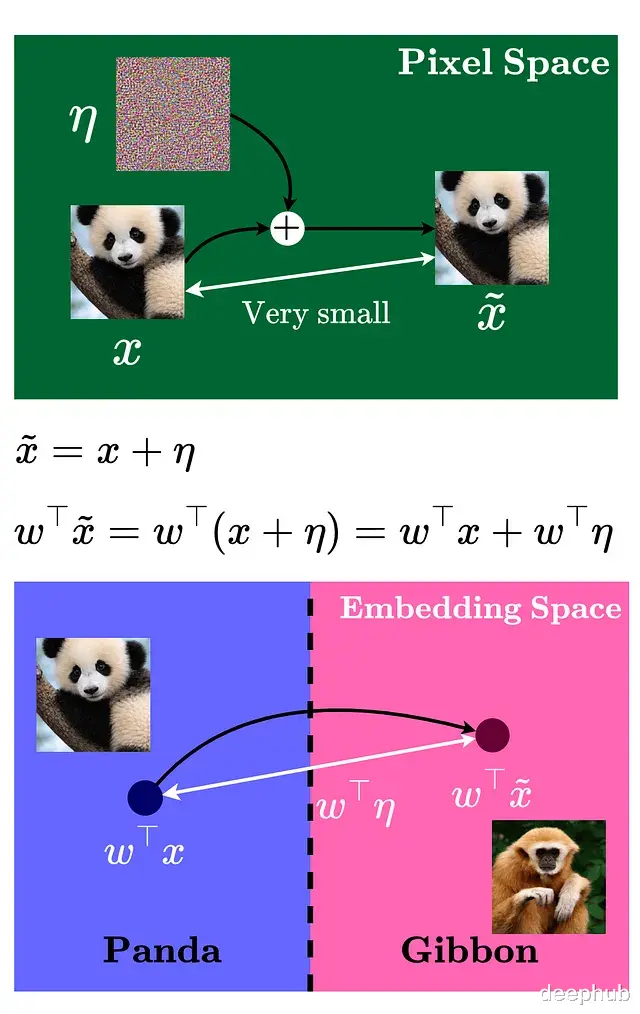
像素空间里的扰动虽小，但经过权重矩阵的放大在嵌入空间产生的效应就明显了，嵌入空间的变化量取决于权重向量与扰动向量的点积。

要让这个点积最大化，就得沿着特定方向移动，或者准确说是沿着权重向量的符号方向。

优化函数可以这样定义，把损失函数改写成泰勒级数的一阶展开形式：

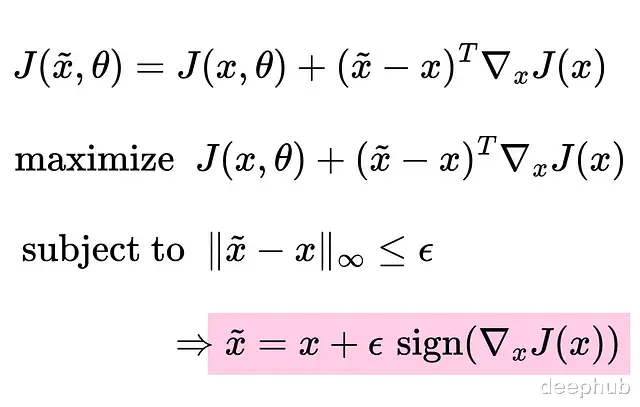
为什么要最大化损失？因为我们的目标是欺骗模型，所以要反着优化的方向走，ε sign()给出了能产生最大更新的方向。

为什么用最大范数而不是别的范数？因为我们的目的是稍微改变输入，并且要控制在人能够感知阈值之下。最大范数让扰动的控制变得精确，这跟真实传感器的情况比较接近。

将最大范数约束在ε以内，就能保证改变幅度不被肉眼发现。这就是快速梯度符号法(Fast Gradient Sign Method, FGSM)的核心思路：利用梯度的符号信息来确定移动方向。

画出数据点周围的决策边界能直观展示FGSM的工作机制。

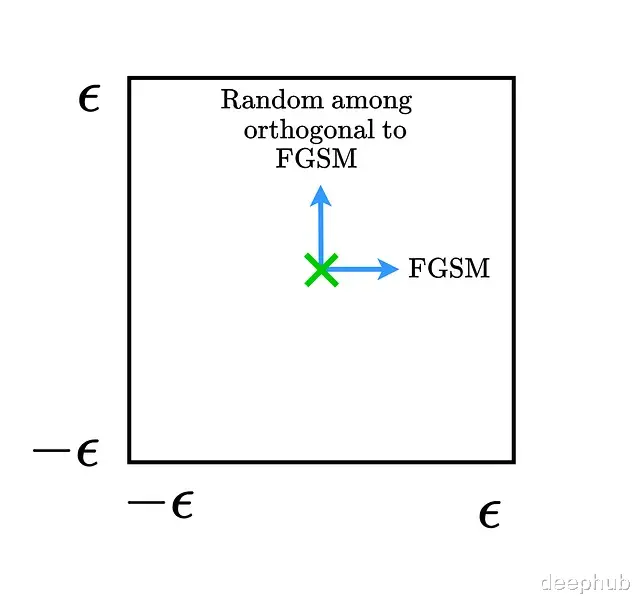
假设沿着FGSM方向和它的正交方向移动，移动范围限制在ε最大范数边界内，用这两个向量把决策空间切成一个二维子空间。

取几个数据点把它们周围的决策边界画出来，白色区域代表正确类别，有色区域对应错误标签。

沿FGSM方向移动会进入错误标签的区域。然后加入随机噪声相当于往随机方向移动：

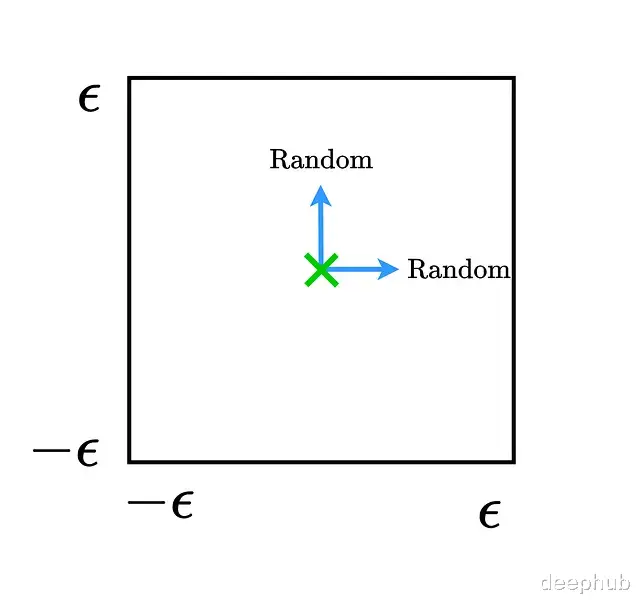
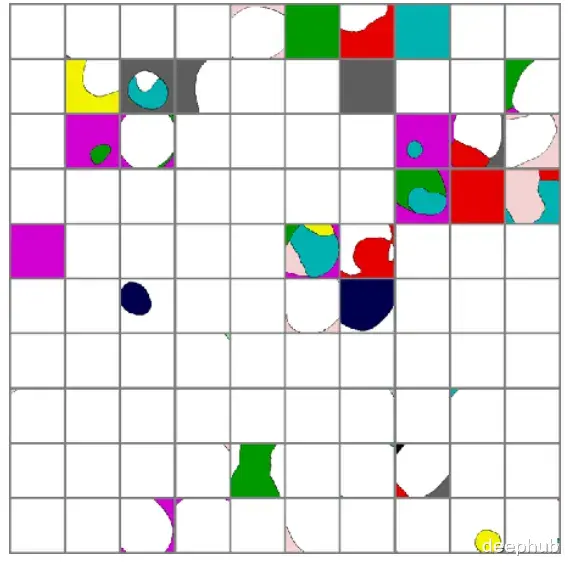
随机方向的移动并不改变数据点的类别归属，这证明了一点：对抗样本不等于随机噪声。

对抗子空间的维度是可以计算的，它表示能用来生成对抗样本的正交方向数量。这些向量和梯度向量之间有较大的点积。

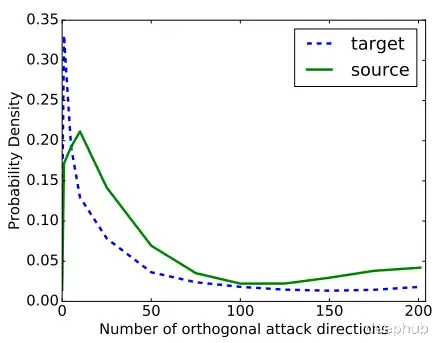
平均下来这些子空间大约有25个正交向量。

另一种思路是直接最大化某个特定目标类别的概率：让输入朝着能够最小化目标标签损失的方向移动。换句话说就是强迫模型认为损失最小的标签就是目标标签，从而输出这个标签。

更新规则写成这样：

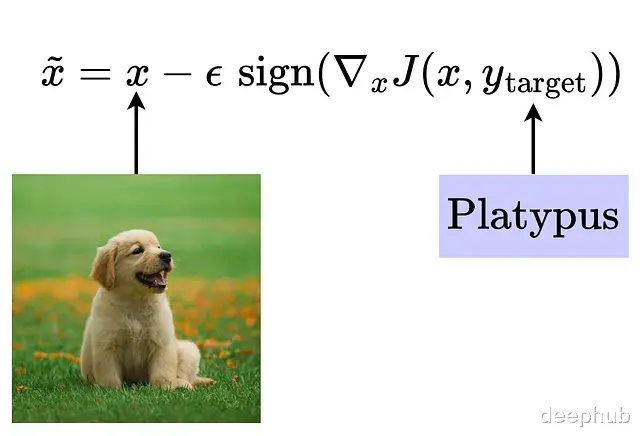
训练一个模型来区分MNIST数据集里的数字3和7。

这是个单层权重的简单线性分类器，权重本身就可以当作梯度用。接下来取权重的符号。

这些权重决定了分类结果。把权重的符号加到样本上或者从样本中减去。

人眼能轻松过滤掉这些图像的背景噪声，但模型会认真对待每一个权重。权重为正时输出7，权重为负时输出3。这些生成的对抗样本彻底瓦解了分类器的判别能力。

机器学习追求的是模型在不同数据集上都能保持稳定表现，这要求模型权重具备泛化能力。既然权重要泛化那基于这些权重生成的对抗样本自然也会泛化。

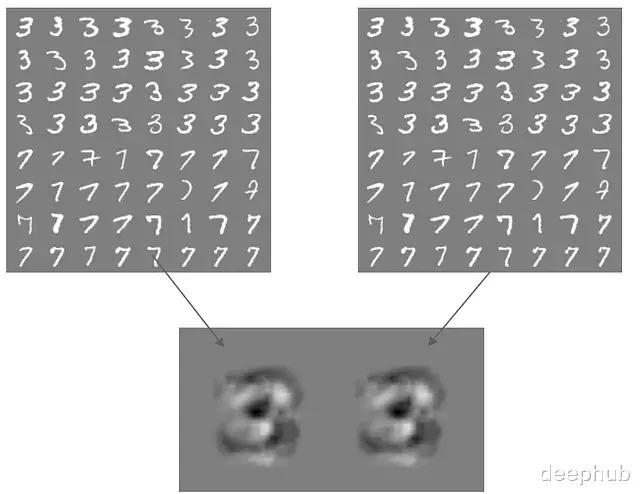
不同数据集应该产生相似的权重分布，可以量化模型间的迁移能力：

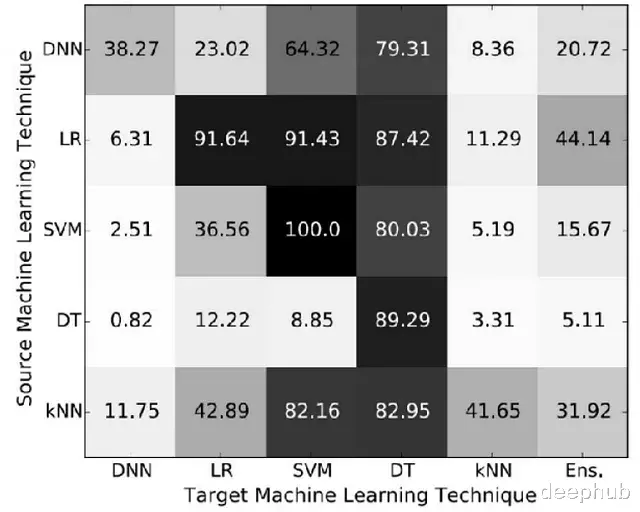
SVM依赖数据特性所以用一个SVM生成的对抗样本很容易攻击另一个SVM，而逻辑回归生成的对抗样本有87.42%的概率能欺骗决策树。

作为攻击者，如果不清楚目标模型的具体架构，可以用模型集成的方式来生成对抗样本。就算拿不到模型的训练数据标签，也能利用模型的输出来构造对抗样本。

有意思的是，人脑也会遭遇类似的"对抗攻击"。下面这个例子挺经典：

这些其实是同心圆，但因为方块的排列方向大脑会把它们解读成螺旋。

用对抗样本训练深度神经网络能起到正则化的作用，还能改善性能。

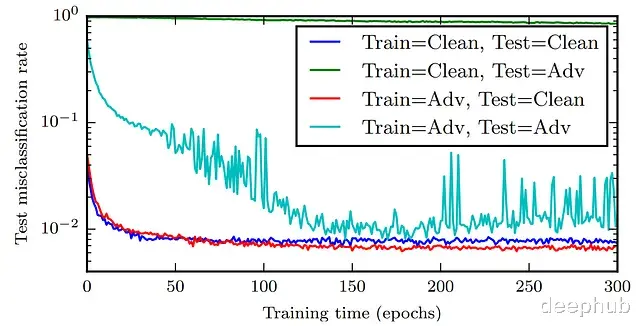
对抗训练确实能提升DNN的表现，损失函数可以重新表述成这种形式：

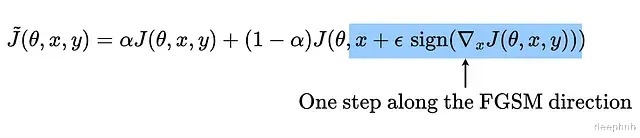
不过严格的线性模型用对抗样本训练不会有什么改进。还可以修改损失函数，给对抗样本分配更高的权重：

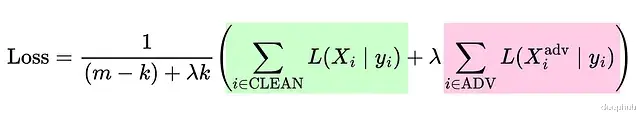
需要明确一点，这些做法都是在和对抗攻击做斗争。要降低对抗攻击的成功率，需要强大的优化算法配合严格的非线性模型架构。

参考文献

Goodfellow, I. J., Shlens, J., & Szegedy, C. (2014). Explaining and Harnessing Adversarial Examples. ArXiv. /abs/1412.6572

Goodfellow, I. J., Mirza, M., Xu, B., Ozair, S., Courville, A., & Bengio, Y. (2014). Generative Adversarial Networks. ArXiv. /abs/1406.2661

Tramèr, F., Papernot, N., Goodfellow, I., Boneh, D., & McDaniel, P. (2017). The Space of Transferable Adversarial Examples. ArXiv. /abs/1704.03453

https://avoid.overfit.cn/post/815495f184a049389d702becdb972067

作者：Kavishka Abeywardana