[LG]《Prior Makes It Possible: From Sublinear Graph Algorithms to LLM Test-Time Methods》A Blum, D Hsu, C Rashtchian, D Saless [Toyota Technological Institute at Chicago & Columbia University & Google Research] (2025)
推理时增强与预训练知识的关系:从亚线性图算法到大语言模型(LLM)推理效率
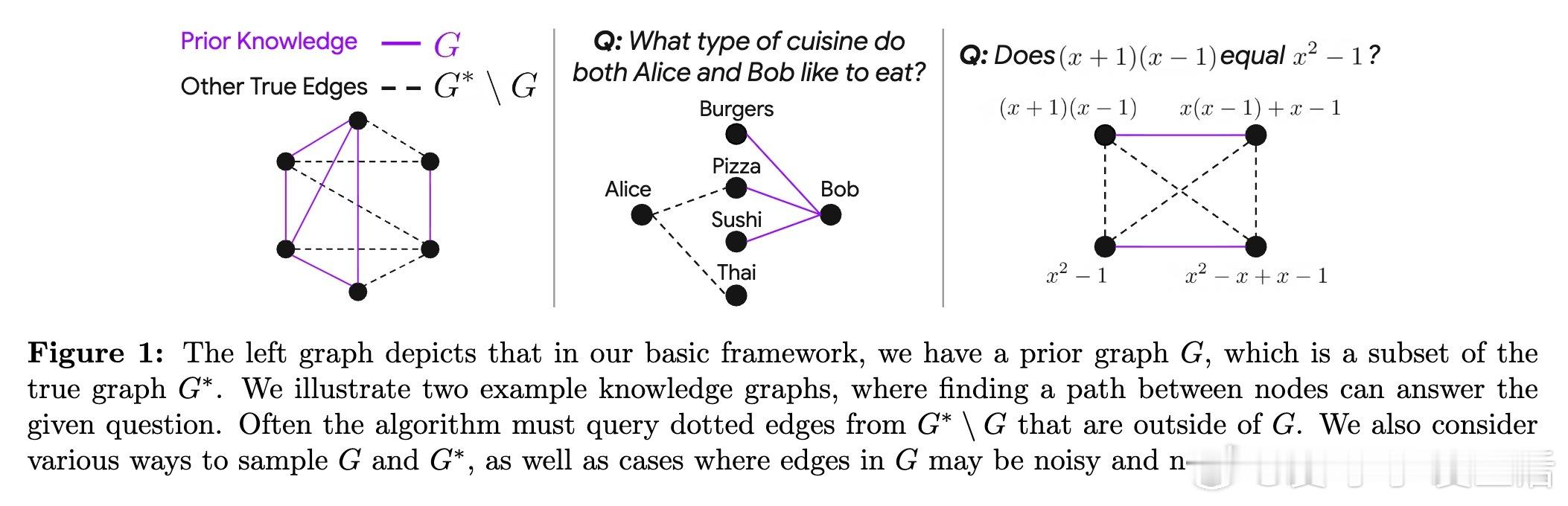
本文提出了一个图论框架,抽象大语言模型的预训练知识为部分且可能带噪的知识子图G,目标知识图为完整图G*。测试时增强(如RAG、工具调用)对应于通过查询“oracle”补充G中缺失的真实边,完成多步推理问题——即寻找G*中两点间的路径。
核心发现:
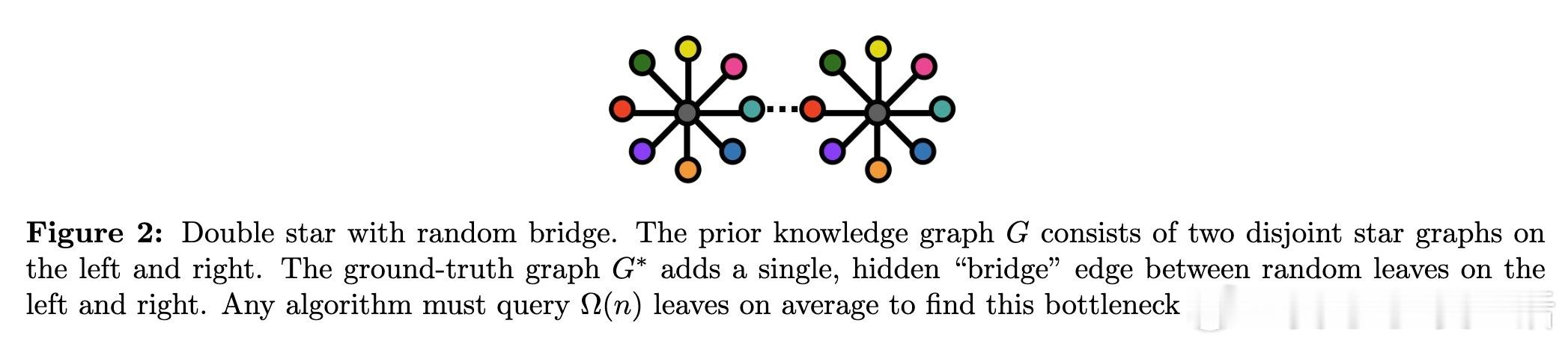
1. 存在“相变”现象:当预训练知识图较为稀疏、仅由多个小连通块组成时,路径发现极其困难,需至少Ω(√n)次查询,效率低下;一旦预训练知识密度超过临界阈值,形成“巨型连通分量”,即可通过常数期望查询次数高效推理。
2. 提出“Retrieval Friendliness”性质,刻画何种先验结构可保证以常数查询复杂度完成准确推理。
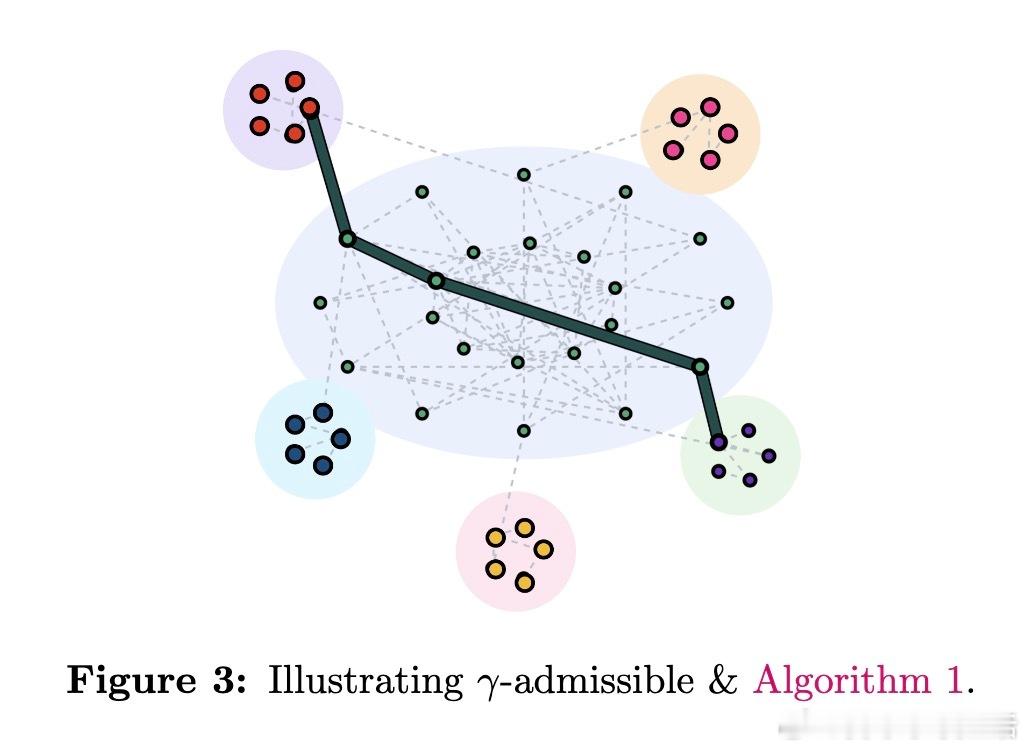
3. 设计双向检索增强算法(BiRAG),在满足“γ-可容性”条件下,实现期望O(1/γ)次查询找到路径。
4. 证明了基于随机图(Erdős–Rényi模型)预训练知识的上下界,揭示了预训练知识密度对推理效率的决定性作用。
5. 讨论了知识可靠性问题,提出多重路径验证以提高推理鲁棒性,并分析了验证器oracle的查询复杂度。
6. 证明了即使路径长度短,若预训练知识不充分,找到路径仍需大量查询,强调预训练知识丰富度对高效推理的重要性。
意义:
- 理论上支持高效RAG依赖于丰富且连通的预训练知识,提示模型设计需兼顾语言理解与世界知识深度。
- 为LLM多步推理和工具使用提供了严谨的复杂度分析和结构条件,指导未来算法优化。
- 连接了随机图理论、亚线性图算法与机器学习推理机制,开辟了理论研究新方向。
未来方向包括:实证验证理论预测、研究更复杂图任务(如最小生成树)、探索更接近实际检索机制的oracle模型等。
详细论文链接:arxiv.org/abs/2510.16609
机器学习 大语言模型 图算法 知识增强 理论分析